后缀自动机 Suffix Automaton

Posted on Edited on

前置知识

自动机的五个部分

  1. alpha 字符集
  2. state 状态集合。另让$null$表示不存在的状态或转移
  3. init 初始状态
  4. end 结束状态集合
  5. trans 状态转移函数：令$trans(s, str)$表示在状态$s$时读入字符串$str$后，所达到的状态。$trans$应具有传递性。

设

  1. 自动机能识别的所有字符串集合Reg(A) ，其中的字符串$x$满足$trans(init, x)\in end$
  2. 从状态$s$开始能识别的字符串 Reg(s)
  3. 后缀自动机SAM，一个能识别母串$S$的所有后缀的自动机。$SAM(x)=true$当且仅当$x$是$S$的后缀。
  4. $trans(init, str)$即从初始状态读入$str$后到达的状态ST(str) （ST是state的缩写)
  5. 母串$S$的所有后缀的集合Suf，从$a$位置开始的后缀Suffix(a)
  6. 母串$S$的所有连续子串的集合Fac，位置为$[l,r)$的子串S[l,r)

分析

SAM的可行性分析

  1. 对于字符串$s$，若$s\in Fac$，则$ST(s)$应存在，这是因为可以在$s$后面加上一些字符使其变成$S$的后缀。反之$s\notin Fac$，则应有$ST(s)=null$以节省空间

  2. 考虑$ST(a)$能识别哪些字符串，即$Reg(ST(a))$。若$x\in Reg(ST(a))$，则$ax\in Suf$，故$ax$是后缀，$x$也是后缀。$Reg(ST(a))$是每次$a$出现后接下来的后缀。设Right(a) 为a每次出现的开区间末位置，则$Reg(ST(a))$完全由$Right(a)$决定。

  3. 对于状态$s$（不是单个字符串），我们关心$Reg(s)$。如果对于$a,b\in Fac$有$Right(a)=Right(b)$，那么可令$ST(a)= ST(b)$。所以一个状态$s$由所有$Right$集合是Right(s) 的字符串组成。

  4. 考虑状态$s$包括的字符串长度，易证若$s$包含长度为$l$,$r$的字符串，那么一定包含长度为$m(l \leq m \leq r)$的字符串。所以这些字符串长度一定可以组成一个区间，设为 [Min(s), Max(s)]

  5. 状态数是线性的。
    　　状态由$Right$集合决定，考虑两个状态$a,b$的$Right$集合$R_a,R_b$。假设$R_a,R_b$有交集，设$r \in R_a \cap R_b$。由于一个子串只能属于一个状态，所以$a$，$b$所表示的子串不会有交集，即由$r$往前不能有长度相同的子串，故$[Min(a), Max(a)]$和$[Min(b), Max(b)]$没有交集，不妨设$Max(a) < Min(b)$，由于$a$，$b$包含的所有串都可以视为$r$往前的子串，故$a$的所有串都是$b$的任意串的后缀。因$b$的任意串都能找到后缀属于$a$，两者$Right$集合又不相等，故$R_b \subset R_a$。那么任意两个状态的$Right$集合要么不相交，要么一个是另一个的真子集。
    　　疾风将以状态为节点，以$Right$包含关系为父子关系构成的树叫 “分裂树”
    　　不考虑字符串这个主题，“分裂树”易证是线性的；实际上，$SAM$的结点个数最多为$2n$。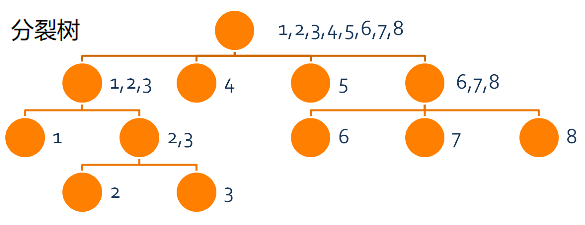

    分裂树举例

  6. 更严谨的分裂树定义：令满足$Right(s) \subset Right(fa)$的最小$|Right(fa)|$的$fa$为状态$s$的父亲。
    　　直观地看，一定是$fa$中最长的字符串向前扩展一位导致了$Right$集合分裂，所以$Max(fa)+1=Min(s)$。

  7. 自动机的边数是线性的。
    　　直观地看，自动机是一个DAG（否则可以无限地在自动机上走，即识别无限长的字符串，显然这是不可能的），而能从$init$走到某个$end$点的肯定是字符串的某一个后缀。字符串只有$n$个后缀，意味着从$init$到$end$只能有$n$种路径；另一方面，节点数只有$O(n)$，所以猜测边数也是$O(n)$的。
    　　标出自动机任意一个生成树，则对于一条非树边$(a\rightarrow b)$，存在若干路径${init \rightarrowtail a \rightarrow b \rightarrowtail e(e\in end)}$对应着一个后缀。对每一个后缀，对应在自动机上走到的第一条非树边。如此每个后缀最多对应一个非树边，而非树边至少被一个后缀对应，所以后缀数量$\geq$非树边数量。所以边数是$O(n)$的。

归纳法构造SAM

SAM的更多性质

这一部分是SAM构造算法的重要依据。
请确认上文所有加粗内容都已理解。

  1. 后缀自动机是一个有向无环图
    $$
    SAM = {分裂树的点，自动机的有向边}
    $$

  2. SAM的构造算法是在线的，即从左到右逐个添加字符。根据数学归纳法，下文假设已有字符串$T$的后缀自动机。

  3. 考虑一个状态$s$，它的$Right(s)={r_1, r_2, \cdots, r_n}$，假如有状态转移$trans(s,c) = t$（即状态$s$后添加一个字符$c$得到状态$t$），由于向右扩展了一位字符，$Right(s)$中只有$T[r_i]=c$的满足要求。所以$Right(t)={r_i+1 | T[r_i]=c}$。
    　　如果$trans(s,c)$存在，那么$trans(Pa(s), c)$必定存在，其中$Pa(s)$表示分裂树上状态$s$的父亲。并且$Right(trans(s,c)) \subseteq Right(trans(Pa(s),c))$。
    　　另一个显然的结论是$Max(s)<Max(t)$。

  4. 后缀自动机没有显式地储存$Right$集合。因此可以认为修改$Right$的时间复杂度为$O(0)$。

  5. 初始状态时母串$T$为空字符串，自动机只有一个节点$root$。

添加一位字符更新自动机

　　令当前字符串为$T$，长度为$L$；末尾添加一个字符$x$，要将$SAM(T)$更新为$SAM(Tx)$。

　　那么新增的子串是$Tx$的所有后缀，可看作$T$的所有后缀后添加了$x$。令$SAM(T)$中表示$T$的后缀的节点为${v_1, v_2, \cdots, v_k=root}$。因为后缀在字符串的末尾出现，所以$L\in Right(v_i)$，可知$v_i$在分裂树上恰好构成一条从叶子到$root$的链，不妨设${v_1, v_2, \cdots, v_k=root}$已经按从叶子到祖先排序。

　　添加字符$x$后，首先新建状态$np$表示$ST(Tx)$，这是一个已确定的状态（因为没有出边），可知$Right(np)={L+1}$。

　　回头考虑旧自动机的$v_i$，设$Right(v_i)={r_1, r_2, \cdots, r_n=L}$。如果能在后面添加字符$x$（注意现在仍是字符串$T$的自动机），即$nv=trans(v_i, x)$存在，我们已经知道$Right(nv)={r_i+1|T[r_i]=x}$；反之如果$v_i$没有$x$的出边，意味着没有$r_i$满足$T[r_i]=x$。由于分裂树上父亲的$Right$扩大，如果$trans(v_i,x)$存在，那么$trans(v_{i+1}, x)$也存在。

　　对于所有$trans(v,x)=null$的$v$，而只有$Tx[r_n=L]=x$满足转移条件，于是添加一条边$trans(v,x)=np$。

　　令$v_p$是$v_1, v_2, \cdots, v_k$中第一个有$x$出边（即$trans(v_p, x)$存在）的状态。令$q=trans(v_p, x)$，注意，现在仍是旧的自动机。我们能不能直接在$Right(q)$中直接插入$L+1$呢？答案是不能。这是因为有可能$Max(q) > Max(v_p)+1$，隐含意思是$q$在”$v_p$末尾添加$x$”的基础上，由于$Right$集合的缩减，纳入了左端更多字符；如果强行在$Right(q)$中插入$L+1$，会导致$Max(q)$减小而丢失了原来的状态，破坏了自动机的正确性。

强行插入的反例

　　如图所示，$v_p$含有的最长字符串是红色5个“A”，但$trans(v_p,x)=q$含有的最长字符串是蓝色7位字符串，如果在$Right(q)$中强行插入$L+1$即变为绿色部分，会使$Max(q)$从7减少到6从而丢失信息。

　　如果足够幸运，$Max(q) = Max(v_p)+1$，就没有上面的问题，我们可以在$Right(q)$中插入$L+1$，然后只要令$Pa(np)=q$即可完成自动机更新。注：理论上$Right(trans(v_p\dots v_k,x))$都要插入$L+1$，但这些状态的出边都没有发生改变，而后缀自动机实际上不记录$Right$，所以更新完成。

　　如果没那么幸运，从图上可知，原状态$q$在插入末尾字符$x$后应转换两个状态，设蓝色对应的状态为$q'$（沿用$q$)，绿色状态为$nq$（新建节点）。显然
$$
trans(q', *) = trans(q, *), \
Pa(q')=nq，\
Right(nq)=Right(q')\cup {L+1}，\
Max(nq) = Max(v_p)+1
$$
显然$Right(nq)$是真包含${L+1}$的最小集合，所以
$$ Pa(np)=nq $$

　　截至目前我们新添了$np$，将$q$转化为$q',nq$，其中$np,q'$都正确处理了出边和分裂树父亲。
那么$nq$的分裂树父亲又是谁呢？结合上图易证
$$ Pa(nq)=Pa(q) $$

$nq$的出边是哪一些？由于新添的最后一个字符不能带来更多的状态转移（最后一个字符后面再没有字符了），所以
$$ trans(nq, *) = trans(q, *) $$

　　最后，我们还要考虑原自动机中指向$q$的状态，和新自动机中应当指向$q'$和$nq$的状态。在$v_p,\cdots,v_k$中，由于$Right$的扩大，$Right(trans(v_i,x))$也逐渐扩大（不缩小），所以只有一段连续的$v_p,\cdots,v_e(e\le k)$是指向$q$的，由于要配合在$Right$集合中插入$L+1$，这些出边要修改为
$$ trans(v_i,x) = nq $$
其余指向$q$的状态必然由于左端有过多字符而无法指向$nq$，于是改为指向$q'$，等效于不做任何修改。

　　最后的最后，对于$v_{e+1},\cdots,v_k$，对于$nv=trans(v_i, x)$，必然可以粗暴地令$Right(nv)$插入$L+1$，所以转移关系可以保持不变，等效于不做任何修改。

标准代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
#include <iostream>
#include <cstring>
using namespace std;

const int MAXW = 26, MAXN = 1e5+2;

struct State {
	State* go[MAXW];
	State* pa;
	int mx;

	State(int MX):pa(0), mx(MX) {
		memset(go, 0, sizeof(0));
	}

	State(const State* o) {
		pa = o->pa;
		memcpy(go, o->go, sizeof(o->go));
		mx = o->mx;
	}
}*last, *root;

void extend(int x) {
	State* p = last;
	State* np = new State(p->mx+1);
	last = np;

	while (p && p->go[x]==0)
		p->go[x] = np, p = p->pa;

	if (p == 0) return np->pa = root, void();

	State* q = p->go[x];
	if (p->mx+1 == q->mx)
		return np->pa = q, void();

	State* nq = new State(q);
	nq->mx = p->mx+1;
	q->pa = np->pa = nq;
	while (p && p->go[x]==q)
		p->go[x] = nq, p = p->pa;
}

char st[MAXN];

int main() {
	scanf("%s", st);

	last = root = new State(0);

	for (int i=0; st[i]!='\0'; ++i)
		extend(st[i]);

	return 0;
}

结束语

　　SAM思路真的异常精妙，环环相扣，巧夺天工。不幸的是优美的结论是以复杂而庞大的论证为代价的。

　　被奉为圣经的2012年noi冬令营陈立杰讲稿(SAM后缀自动机)在描述构造过程的时候没有解释可以省略的操作为什么被省略，导致思路有很大残缺和跳跃。即使是本文也用了不少“显然”字眼，但比较原文已有较大改进。另外，原讲稿没有交代构造算法为什么是$O(n)$的。疾风理解这ppt花了整整三天如果本文对你有帮助，不妨赏疾风一支冰阔乐喝（馋.jpg）

　　有人说SAM完全可以当做黑盒来用，我认为不然。黑盒SAM的唯一功能是判定子串是否存在，局限性很大。而SAM的实战应用代码相对裸构造有很大增改，例如要结合dfs序，平衡树，动态树等等技巧，且都是建立在完全理解后缀自动机的基础上，难度依然很大。这部分日后再填补。

转载请注明原作者和网址