SAM实战剖析

Posted on 2020-10-11 Edited on 2022-10-13

实战不会SAM？导致比赛打铁？快点学！

前置知识

后缀自动机(Suffix-Automaton)

在自动机上游走

从$root$开始，沿目标字符串逐个字符走。若路径存在，即当前子串存在；反之，若出边不存在，即目标子串不存在。

求最小表示

求字符串$S$的最小表示。

度娘有$O(n)$的特殊做法，此处不赘述。

构造字符串$SS$的后缀自动机，从$root$开始，每次沿最小的出边走，走n步就得到了$SS$中长度为n的最小子串，即$S$的最小表示。

求本质不同的第k小子串

SPOJ SUBLEX 题意：求字符串$S$的所有本质不同子串中的第$k$小。$length(S)\le 9e4, 询问数量\le 500$。

SAM构造完成后得到一个DAG，利用拓扑序求从每个点出发可能的路径数目。见拓扑排序的方法。最后用类似二分法求第k小即可。

// 内存池+计数排序的SAM，相对优秀
#include <algorithm>
#include <iostream>
#include <cstring>
using namespace std;

const int MAXW = 26, MAXN = 9e4+5;

struct State {
    State *pa;
    State *go[MAXW];
    int Max;
    
    int siz = 1;
    
    static int cnt;    
}sam[MAXN<<1], *last, *root;

State* alloc(int Max) {
    State& ref = sam[State::cnt++];
    ref.Max = Max;
    return &ref;
}

State* alloc(State* src) {
    State& ref = sam[State::cnt++];
    ref = *src;
    return &ref;
}

void extend(int c) {
    State *p = last, *np = alloc(p->Max+1);
    last = np;
    
    while (p && !p->go[c])
        p->go[c] = np, p = p->pa;
    
    if (!p) return np->pa = root, void();
    
    State* q = p->go[c];
    if (q->Max == p->Max+1)
        return np->pa = q, void();
    
    State* nq = alloc(q);
    nq->Max = p->Max + 1;
    q->pa = np->pa = nq;
    while (p && p->go[c] == q)
        p->go[c] = nq, p = p->pa;
}

int State::cnt = 0;

char st[MAXN];
int Q, len;

int num[MAXN];
State* b[MAXN<<1];

// 类似二分法求当前第lef小
void dfs(const State* now, int dep, int lef) {
    static char ans[MAXN];
    if (lef == 0) {
        ans[dep] = '\0';
        puts(ans);
        return;
    }
    
    for (int i=0; i<MAXW; ++i) if (now->go[i]) {
        const State* g = now->go[i];
        if (lef <= g->siz) {
            ans[dep] = i+'a';
            return dfs(g, dep+1, lef-1);
        } else {
            lef -= g->siz;
        }
    }  
}

int main() {
    #ifdef DEBUG
    freopen("in", "r", stdin);
    #endif
    
    last = root = alloc(0);
    
    scanf("%s", st);
    for (int &i=len; st[i]!='\0'; ++i) {
        st[i] -= 'a';
        extend(st[i]);
    }
    
    // 拓扑排序
    for (int i=0; i<State::cnt; ++i) ++num[sam[i].Max];
    for (int i=len-1; i>=0; --i) num[i] += num[i+1];
    for (int i=0; i<State::cnt; ++i) b[--num[sam[i].Max]] = &sam[i];
    // 沿拓扑序DP
    for (int i=0; i<State::cnt; ++i)
        for (int j=0; j<MAXW; ++j)
            if (b[i]->go[j])
                 b[i]->siz += b[i]->go[j]->siz;
    
    scanf("%d", &Q);
    while (Q--) {
        int aim;
        scanf("%d", &aim);
        dfs(root, 0, aim);
    }
    
    
    return 0;
}

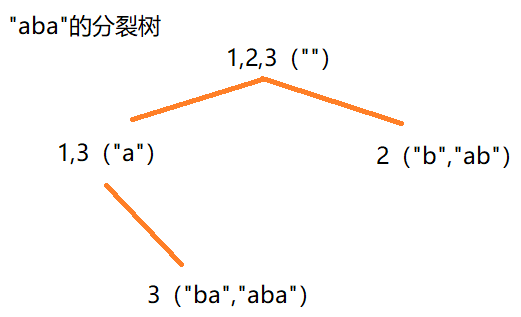
离线计算|Right|

构造好的后缀自动机隐含了一颗分裂树，只需访问所有节点和$Pa$指针，就能还原这颗分裂树。显然，叶子节点的$|Right| = 1$，但仅有这些信息还不足推出其他节点的$|Right|$，这是因为节点在往下分裂时可能丢失元素

"aba"的分裂树。“1”没有出现在叶节点中

如上图所示，“1”在分裂的过程中消失了，不存在叶子节点中。

为什么$Right$集合的元素无法往下分裂？这是因为它表示的子串无法向左端扩展，换句话说，它是前缀。注意到叶子节点也是前缀。综上所述，只要对前缀所在节点的$|Right|$预置为$1$（其他节点预置为$0$），然后自底向上更新分裂树即可得到所有$|Right|$

分裂树上拓扑排序

上文引出了一个新问题，如何自底向上地访问分裂树？一种直观的办法是bfs收集SAM所有节点再做拓扑排序，这逻辑复杂而代码繁琐。一种更好的办法是，在构造SAM时采用内存池技术，之后对内存池按照$Max$降序排序即可。原因是
$$ Max(fa)+1=Min(s) \Rightarrow Max(s) > Max(fa)$$
有趣的是，分裂树的拓扑序也是自动机的拓扑序！原因是
$$ trans(s, *)=t \Rightarrow Max(t) > Max(s) $$
如果你忘记了，请复习后缀自动机的更多性质。

拓扑排序要点

指针板构造采用内存池技术
$Max$可能的取值仅有$[1,n]$，所以要采用计数排序
不要真的修改内存池，而是新开指针做排序
如果不得不写常规拓扑排序，bfs时请注意DAG的重复访问

for (int i=0; i<cnt; ++i) ++num[sam[i].Max];
for (int i=len-1; i>=0; --i) num[i] += num[i+1];
for (int i=0; i<cnt; ++i) b[--num[sam[i].Max]] = &sam[i];
// sam[] has been top sorted by b[].

剩余细节在例题1、例题2中体现

求长度为i的子串的最大出现次数

SPOJ NSUBSTR 题意：给出字符串S（长度<=2.5e5），设f(x)为S中长度为x的子串的最大出现次数，求f(1...length(s))。

分析：后缀自动机中每个状态$s$蕴含的字符串长度为$[Min(s), Max(s)]$，每个出现了$Right(s)$次，只需用$|Right(s)|$更新$ans[Max(s)]$就行了，在最后输出前依次用$ans[i+1]$更新$ans[i]$即可。原因是长度更长的子串出现的次数一定不超过长度短的。

// 朴素的拓扑排序版本，推荐改用计数排序
#include <algorithm>
#include <iostream>
#include <cstring>
using namespace std;

#ifdef DEBUG
const int MAXW = 26, MAXN = 50+3;
#else
const int MAXW = 26, MAXN = 250000+3;
#endif

struct State {
    State* pa;
    State* go[MAXW];
    int Max;
    
    int RSiz = 0, inD = 0;
    bool vis = false;
    
    State(int Max) {
        memset(go, 0, sizeof(go));
        pa = nullptr;
        this->Max = Max;
    }
    
    State(const State* o) {
        memcpy(go, o->go, sizeof(go));
        pa = o->pa;
        Max = o->Max;
    }
}*root, *last;

void extend(int c) {
    State *p = last, *np = new State(p->Max+1);
    last = np;
    
    while (p && !p->go[c])
        p->go[c] = np, p = p->pa;
    
    if (!p) return np->pa = root, void();
    
    State *q = p->go[c];
    if (p->Max+1 == q->Max)
        return np->pa = q, void();
        
    State *nq = new State(q);
    q->pa = np->pa = nq;
    nq->Max = p->Max + 1;
    while (p && p->go[c] == q)
        p->go[c]=nq, p = p->pa;
}

char st[MAXN];
int len;

State* q[MAXN<<1];
int cnt = 0;

void bfs() {
    q[0] = root;
    cnt = 1;
    
    for (int i=0; i<cnt; ++i) {
        State* const now = q[i];
        if (now->pa) ++now->pa->inD;
        for (int j=0; j<MAXW; ++j)
            if (now->go[j] && !now->go[j]->vis) {
                q[cnt++] = now->go[j];
                now->go[j]->vis = true;
            }
    }
}

void topsort() {
    int head = 0, tail = partition(q, q+cnt, [](const State* o) {
        return o->inD == 0;
    }) - q;
    
    while (head < tail) {
        State* now = q[head++];
        if (!now->pa) continue;
        now->pa->RSiz += now->RSiz;
        if (--now->pa->inD == 0)
            q[tail++] = now->pa;
    }
}

int ans[MAXN];

int main() {
    #ifdef DEBUG
    freopen("in", "r", stdin);
    #endif
    
    root = last = new State(0);
    
    scanf("%s", st);
    for (int &i=(len=0); st[i]!='\0'; ++i) {
        st[i] -= 'a';
        extend(st[i]);
    }

    // bfs取出SAM中的所有节点，注意判重
    bfs();
    
    // 对SAM中所有蕴含前缀的状态 |Right| = 1（其它置为0）
    State* p = root;
    for (int i=0; i<len; ++i) {
        p = p->go[st[i]];
        ++p->RSiz;
    }

    // 拓扑排序，顺便自底向上更新|Right|
    topsort();

    for (int i=0; i<cnt; ++i) {
        ans[q[i]->Max] = max(ans[q[i]->Max], q[i]->RSiz);
    }
    
    for (int i=len; i>1; --i)
        ans[i-1] = max(ans[i-1], ans[i]);
    
    for (int i=1; i<=len; ++i)
        printf("%d\n", ans[i]);
    
    return 0;
}

跳向父亲，舍弃左端，寻求匹配

now = now->pa的本质是抛弃左端一部分字符，带来的效果是$Right$集合的扩张。这个特性在求最长公共子串的时候尤为好用，与KMP舍弃右端部分字符以寻求匹配的原理有异曲同工之妙。

求两字符串的最长公共子串

SPOJ LCS 题意：求字符串$S1,S2$的最长公共子串(要求连续)

分析：后缀自动机很擅长处理连续串的匹配。试想我们做出$S1$的SAM，然后直接跑$S2$，势必出现出边不存在的问题——无法继续匹配了。不妨设无法继续匹配时，导致无法匹配的字符是$S2[i]$，当前状态为$s$，即$trans(s, S2[i])$不存在，即不存在$S1[r_j]=S2[i], r_j\in Right(s)$。想要寻求匹配，只能抛弃已匹配的子串左端，而s=s->pa恰好带来了最少的抛弃量，使得$Right(s)$能扩张，从而带来匹配的可能性。

换句话说，当s->go[S2[i]] == nullptr时，重复s = s->pa，直到获得匹配s->go[S2[i]] != nullptr或不可能匹配s == nullptr。

假如直接能匹配呢？那太简单了，匹配长度加一，下一位。

于是最终解为：记当前已匹配长度$match$，当前答案$ans$，当前自动机状态$s$，接下来尝试匹配$S2[i]$，若$trans(s,S2[i])$存在，就转移，并且$match$加一；否则尝试不断跳分裂树的$fa$，直到转移存在，由于$Max(fa) < Min(s) \le match$，$match$必能取到$Max(fa)$，所以$s$跳到$trans(fa, S2[i])$， $match$取为$Max(fa)+1$即可。每走一步都用$match$更新$ans$。

// 省略SAM的构造和其他乱七八糟的东西
    State* now = root;
    int match = 0, ans = 0;
    for (int i=0; sb[i]!='\0'; ++i) {
        const int c = (sb[i]-='a');
        
        if (now->go[c]) {
            now = now->go[c];
            ++match;
        } else {
            while (now && !now->go[c])
                now = now->pa;
            if (now) {
                match = now->Max+1;
                now = now->go[c];
            } else {
                now = root;
                match = 0;
            }
        }
        
        ans = max(ans, match);
    }